The Mullins effect is the stress-softening observed in rubber when it is loaded for the first time to a given strain. On subsequent loadings to the same strain, the rubber shows lower stress.

Once “damaged” by a prior stretch, the rubber never quite goes back to its original stiffness.

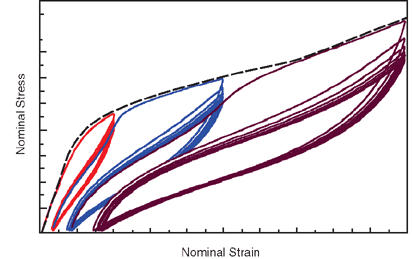
Image from: https://abaqus-docs.mit.edu/2017/English/SIMACAEMATRefMap/simamat-c-mullins.htm

What’s happening?

Unlike the Payne effect (filler network breakdown at small cyclic strains), the Mullins effect involves large deformations and changes inside the rubber matrix itself:

Key mechanisms include:

• Breakage of weak polymer–filler bonds

• Slippage or rearrangement of polymer chains

• Micro-damage in the filler–rubber network

• Possible chain scission at very high strains

After the first loading:

• Some internal structure is permanently altered

• Reloading follows a softer stress–strain path

• The effect depends on the maximum strain previously experienced

How it appears experimentally

In a uniaxial tensile test:

1. First loading → high stress

2. Unloading → hysteresis (energy loss)

3. Reloading to same strain → lower stress curve

4. Loading beyond previous maximum strain → stiffness increases again until a new “damage level” is reached

This creates a characteristic stress–strain loop.

Key characteristics

• Strain-history dependent

• Partially irreversible

• Occurs in filled and unfilled rubbers, but is much stronger in filled systems

• Strongly tied to energy dissipation (hysteresis)

Why it matters in real applications

The Mullins effect impacts:

• Dimensional stability

• Fatigue life

• Sealing performance

• Load–deflection behavior

• First-cycle vs in-service properties

Examples:

• Rubber seals feel “softer” after initial installation

• Tires experience property changes after first use

• Vibration isolators shift stiffness after commissioning

Factors that influence the Mullins effect

• Filler content and type

• Quality of filler dispersion

• Polymer–filler interaction strength

• Maximum strain level

• Temperature

• Strain rate

Unlike the Payne effect, resting the material does not fully restore the original stiffness.

Mullins vs. Payne (side-by-side)

Modeling the Mullins effect

Common approaches in constitutive models:

• Damage mechanics models

• Pseudo-elastic models (e.g., Ogden–Roxburgh model)

• Energy-based softening formulations

These are essential in finite element analysis of rubber components.