The Payne effect is a classic (and very important) phenomenon in filled rubber materials, especially those reinforced with carbon black or silica.

In short: when you cyclically deform a filled rubber at small to moderate strains, its storage modulus (G′) drops as strain amplitude increases. That strain-dependent softening is the Payne effect.

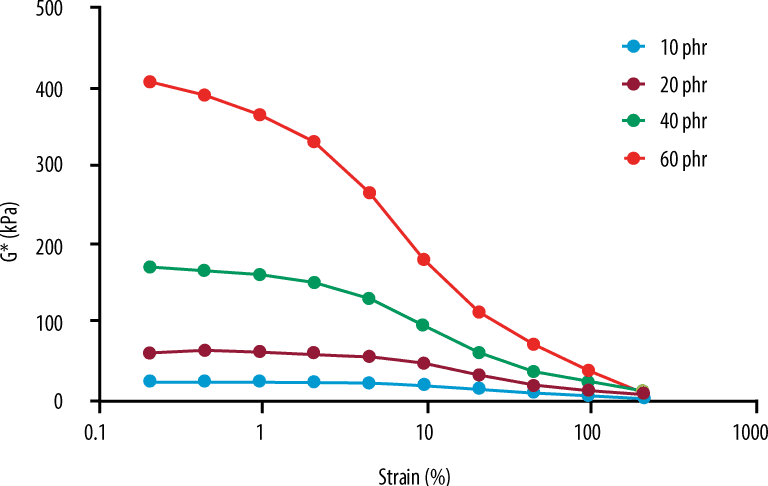
Image from: https://www.rubber-testing.com/products/moving-die-rheometer/d-rpa-3000

What’s actually happening

In filled rubbers, you don’t just have polymer chains—you also have a filler network:

• Filler particles (carbon black, silica) form weak, physical connections with each other.

• At very small strains, this filler–filler network is intact → high stiffness (high G′).

• As strain increases:

  • The filler network progressively breaks down

  • Rubber becomes softer

  • G′ decreases, while loss modulus (G″) often increases

This breakdown is reversible: if you reduce the strain and let the material rest, the filler network partially reforms.

How to measure the Payne effect

Typically observed using dynamic mechanical analysis (DMA) or a rubber process analyzer (RPA):

• Apply oscillatory shear

• Sweep strain amplitude (e.g., 0.01% → 100%)

• Measure:

  • Storage modulus (G′)

  • Loss modulus (G″)

  • Tan δ

The Payne effect is often quantified as:

ΔG′=G′low strain−G′high strain\Delta G′ = G′_{\text{low strain}} - G′_{\text{high strain}}ΔG′=G′low strain​−G′high strain​

A larger ΔG′ → stronger Payne effect.

Here a nice video from MonTech (not sponsored)

Payne effect in rubber products

The Payne effect strongly influences:

• Tire performance

  • Rolling resistance

  • Wet grip

  • Noise

• Vibration damping

• Fatigue and durability

• Processability during mixing and shaping

For example:

• High Payne effect → strong filler network → good reinforcement but higher hysteresis

• Low Payne effect → better dispersion → lower energy loss (important for low-rolling-resistance tires)

What affects the Payne effect

• Filler type

  • Carbon black vs. silica

  • Surface area and structure

• Filler loading

  • Higher loading → stronger effect

• Dispersion quality

  • Poor dispersion → larger Payne effect

• Polymer–filler interaction

  • Silane coupling agents (for silica) reduce the effect

• Temperature and frequency

Payne effect vs. Mullins effect (quick contrast)

• Payne effect:

  • Small strain, cyclic, dynamic

  • Filler network breakdown

• Mullins effect:

  • Large strain, quasi-static

  • Stress softening of the rubber matrix

They’re related but not the same phenomenon.